平面机构运动简图及其自由度
第一节 基本概念
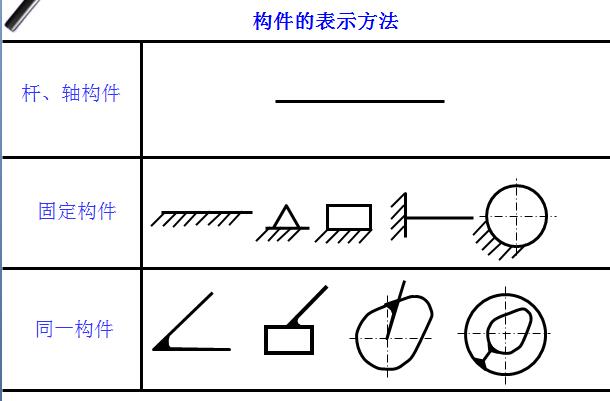
一、构件(Link)
机械的运动单元,传递运动和力的载体。
实例:内燃机中的缸体、活塞、连杆、曲轴等。
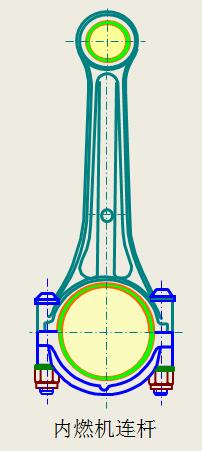
一个构件也可以由几个零件刚性联接组成。
实例:连杆由连杆体、轴瓦、连杆盖、螺栓、垫圈、螺母、连杆衬套等相互刚性联接组成。

零件(Part)是机械的制造单元。
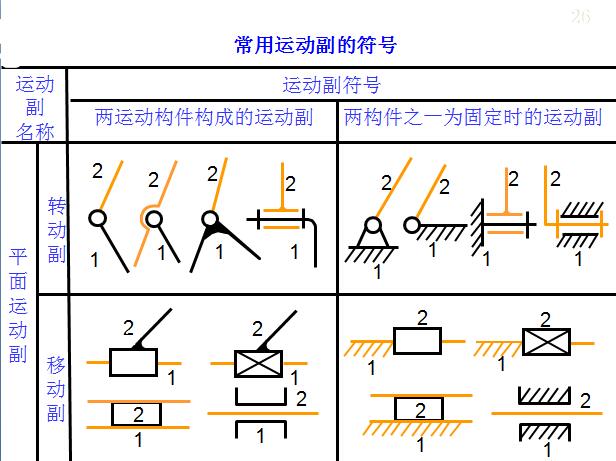
二、运动副(Kinematic pair)
运动副 构件之间的可动联接
运动副元素 两构件上参与接触而构成运动副的部分
三、自由度、约束
自由度(Degree of freedom,Mobility) 构件间的独立相对运动

v 在平面内作自由运动的构件具有3个独立的相对运动;在三维空间作自由运动的构件具有6个独立的相对运动。
约 束(Constraint) 运动副对构件间相对运动的限制作用v对构件施加的约束个数等于其自由度减少的个数。
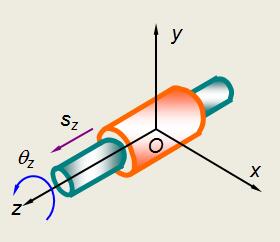
一个完全独立的刚体在空间直角坐标系下的自由度为sx,sy,sz,qx,qy,qz,即自由度数f =6。
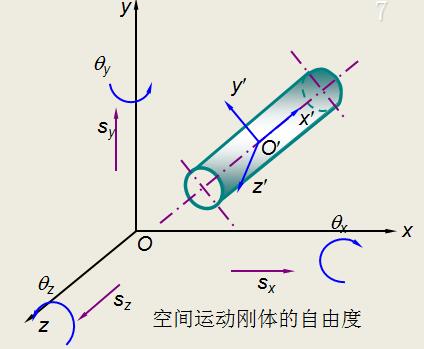
平面运动刚体的自由度为sx,sy,qz,即自由度数 f =3。

观察图示两构件组成的圆柱副(Cylindric pair)
两构件保留的相对运动sz和qz,即自由度数f = 2。两构件之间受限制的相对运动sx,sy,qx和qy,即约束数 s = 4。两构件之间可以传递的力(力矩)Px,Py,Mx,My 结论:几何约束与力约束本质上是一致的,是可以相互替代的。
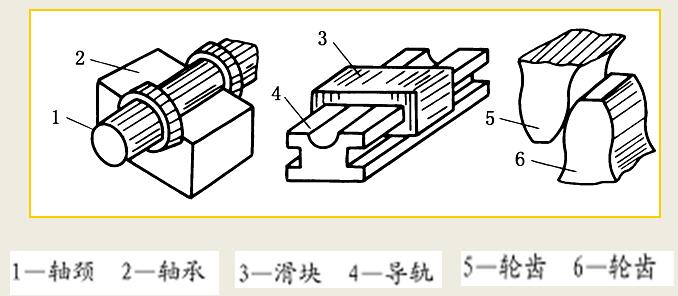
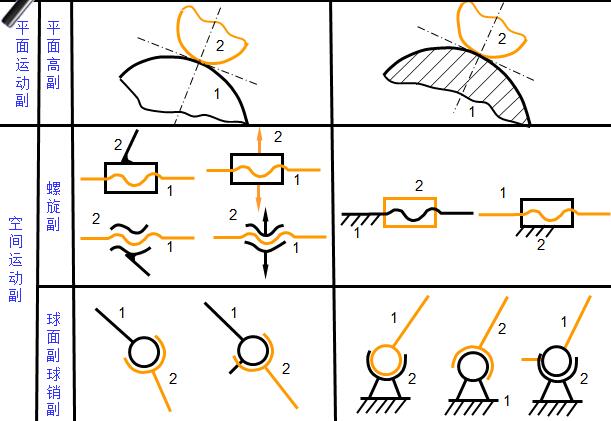
构件的不同接触形式
点接触(Point contact) 线接触(Line contact)
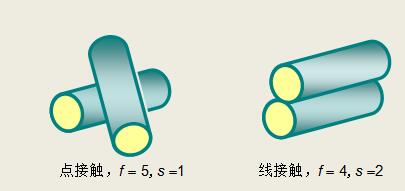
特点
具有较多的自由度,易于构件的自动调整,保持静定特性。
接触应力大,易变形、易磨损、承载能力低。
制造比较困难。
适用场合
结构简单,运动精度要求较高,受力较小。
面接触(Area contact)
特点
相当于多点接触,承载能力较高,应用广泛。
运动副的自由度一般较低,其接触状况对尺寸、形状及相对位置误差十分敏感,实际接触及受力状况难以准确确定,需要较高的制造精度。
保证运动副可靠工作的措施
提高表面硬度
正确选用材料
添加润滑剂
加入中间体,将滑动摩擦改为滚动摩擦
四、运动副的分类
●按运动副引入的约束数分类
I级副(Class I kinematic pair)、II级副、III级副、IV级副、V级副。
●按运动副的接触形式分类
面与面接触的运动副—低副(Lower pair)
点、线接触的运动副—高副(Higher pair)
●按两构件相对运动的形式分类
平面运动副(Planar kinematic pair)
空间运动副(Spatial kinematic pair)
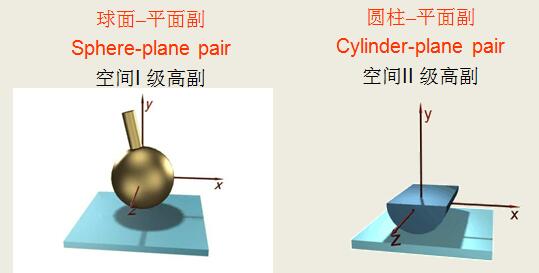
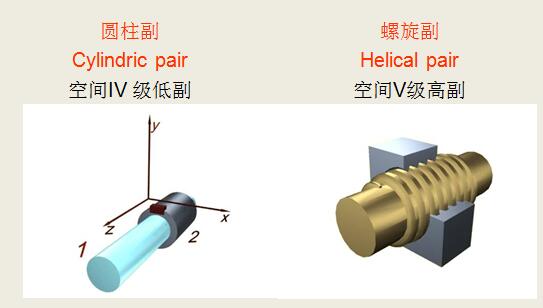
●按接触部分的几何形状分类
圆柱副、球面副、螺旋副、球面–平面副、平面–平面副、球面–圆柱副、圆柱–平面副等等。
运动副举例


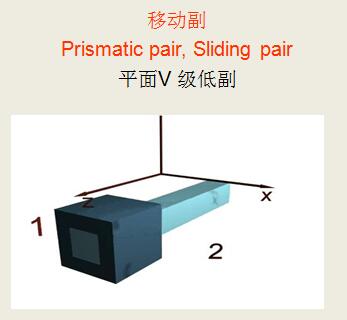
平面机构是应用最广泛的机构。
平面运动副的约束数为1£s£2。
点、线接触的平面运动副—平面高副
面接触的平面运动副—平面低副
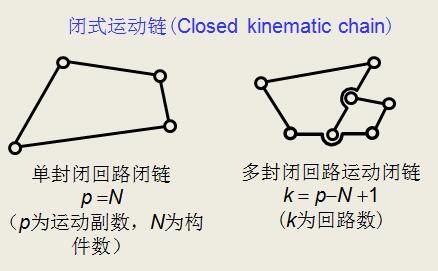
运动链(Kinematic chain)
两个以上构件用运动副联接的构件系统。

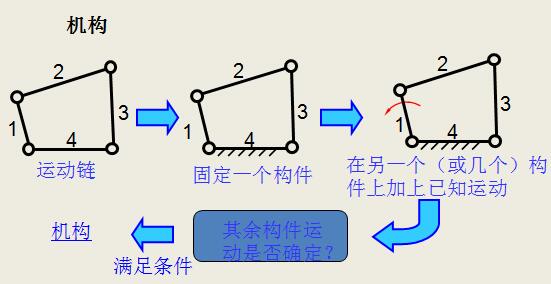
五、机构
机构 在运动链中,若选定某构件为机架,且各构件具有确定的相对运动,则称该运动链为机构。
平面机构
机构中各构件的运动平面互相平行。
空间机构
机构中至少有一构件不在相互平行的平面上运动,或至少有一构件能在三维空间中运动。
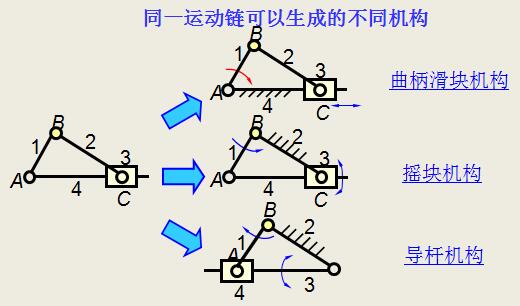
运动链的生成是创造、获取新机构的重要手段。
第二节 平面机构运动简图(自学)
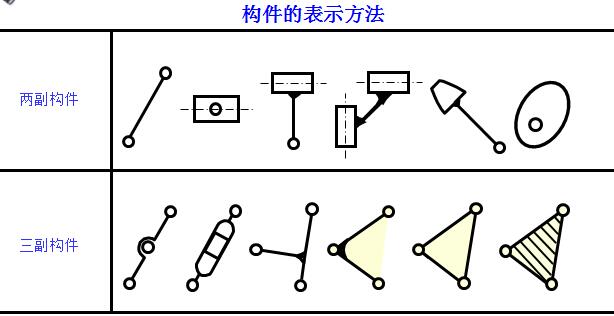
一、构件的类型
原动件(Driving link)—机构中按给定运动规律运动的构件,也称为输入构件(Input link)。
从动件(Driven link, Follower)—其余的可动构件。具有预期的运动规律、对外完成某种工艺动作的从动件也称为输出构件(Output link)或执行构件(Executive link)。
机架(Fixed link,Frame)—固定不动的构件。

根据机构中各构件的相对运动是否在同一平面或平行平面内,可将机构分为平面机构(Planar mechanism)和空间机构(Spatial mechanism)。
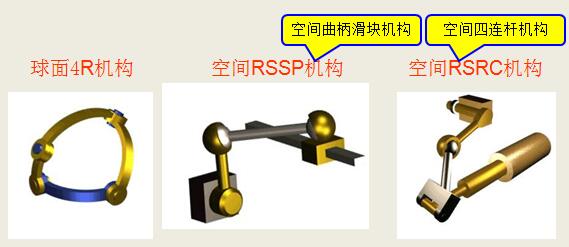
平面机构是我们的主要研究对象。
二、运动简图
机构运动简图(Kinematic sketch)是从运动学角度出发,将实际机械中与运动无关的因素加以抽象和简化后,得到的反映实际机械的运动特性和运动传递关系的图形。
机构运动简图应满足的条件:
⑴构件数目与实际机构相同;
⑵运动副的性质、数目与实际机构相符;
⑶运动副之间的相对位置以及构件尺寸与实际机构成比例。
机构示意图为不严格按比例绘制的简图,用于表达机械的结构特征。

2.机构运动简图的绘制
步骤:
⑴分析机械的动作原理、组成情况和运动情况,确定原动件、机架、执行部分和传动部分。
⑵沿着运动传递路线,逐一分析每两个构件间相对运动的性质,确定运动副的类型和数目。
⑶选择与机械多数构件的运动平面平行的平面,作为机构运动简图的视图平面。
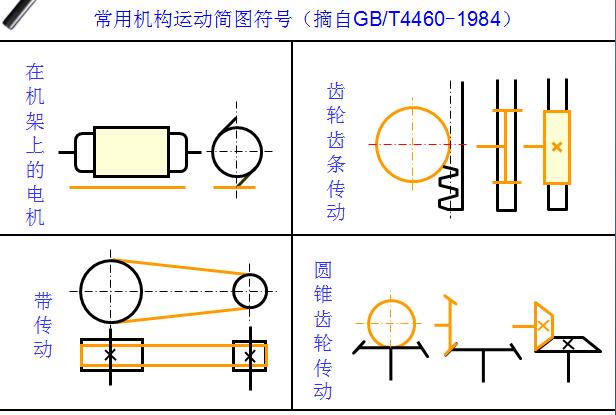
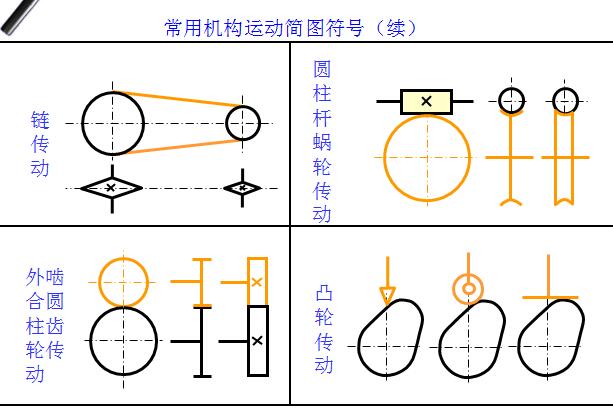
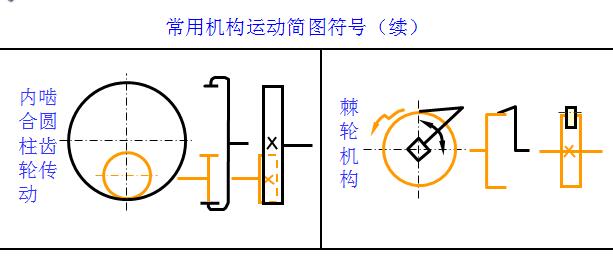
⑷选择适当的机构运动瞬时位置和比例尺ml(m/mm),定出各运动副的相对位置,并用各运动副的代表符号、常用机构的运动简图符号和简单线条,绘制机构运动简图。
⑸从原动件开始,按运动传递顺序标出各构件的编号和运动副代号。在原动件上标出箭头以表示其运动的方向。
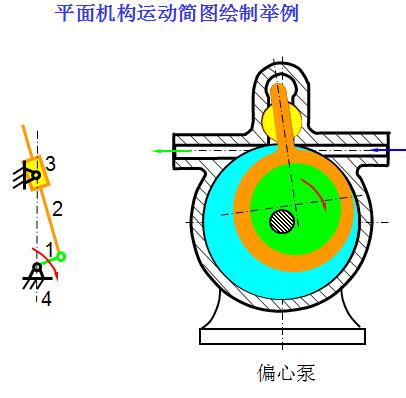
第三节 平面机构的自由度
机构的自由度:机构具有确定运动时所给定的独立运动参数的数目。
一、运动链自由度计算公式

二、运动链成为机构的条件
三、计算平面机构的自由度应注意的事项
1、运动链的自由度计算
运动链的自由度—确定运动链中各构件相对于其中某一构件的位置所需的独立参变量的数目。
考察由N个构件组成的运动链,活动构件数n=N-1。
空间运动


运动链自由度计算举例
例1 缝纫机脚踏板运动链自由度计算
分析:n= 3,p5= 2,p4 = 1,p3 = 1
计算:F=6´3-(3´1+4´1+5´2) =1
只要给定1个独立位置参数,各构件间的相对位置关系就确定了。
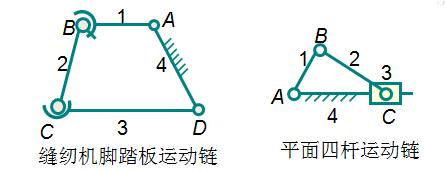
例2平面四杆运动链自由度计算
分析:n = 3,q = 3,p5 =4
计算:F= 3n - 2pL -pH =3´3-2´4 =1
只要给定1个独立位置参数,各构件间的相对位置关系就确定了。
2、运动链成为机构的条件
判断所设计的运动链是否能成为机构,是提出新的设计方案时自行评价方案可行性的关键步骤。
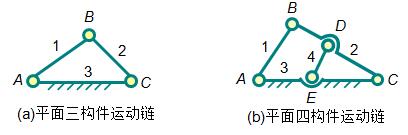
(a) F=3n-2PL-PH=3*2-2*3=0
运动链为一刚性桁架,不能成为机构。
(b) F=3n-2PL-PH=3*3-2*5=-1
该运动链约束过多,成为超静定桁架,不能成为机构。
运动链成为机构的首要条件: 运动链自由度必须大于零。

在F>0的条件下,进一步判断运动链是否具有确定的运动。
例:平面五杆运动链
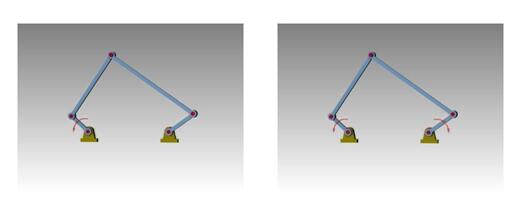
F=3n-2PL-PH =3*4-2*5 =2
原动件数<F,运动链内部的运动关系不确定。运动链不能成为机构。
原动件数=F,运动链内部各构件运动关系确定。运动链成为机构。
例:平面四杆运动链
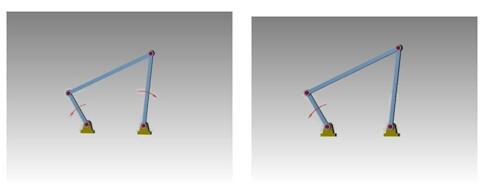
F=3n-2PL-PH=3*3-2*4 =1
原动件数>F,运动链内部的运动关系将发生矛盾,其中最薄弱的构件将会损坏。运动链不能成为机构。
运动链成为机构的条件是:取运动链中一个构件相对固定作为机架,运动链相对于机架的自由度必须大于零,且原动件的数目等于运动链的自由度数。
满足以上条件的运动链即为机构,机构的自由度可用运动链自由度公式计算。
3、计算机构自由度时应注意的问题
● 局部自由度(Passive degree of freedom)
定义:机构中某些构件所具有的仅与其自身的局部运动有关的自由度。

未考虑局部自由度时的机构自由度计算。
F=3n-2pL-pH=3´3-2´3-1=2
考虑局部自由度时的机构自由度计算。
设想将滚子与从动件焊成一体
F=3*2-2*2-1=1
计算时减去局部自由度FP
F=3*3-2*3-1-1(局部自由度)=1
● 复合铰链(Compound hinges)
定义:两个以上的构件在同一处以转动副联接所构成的运动副。
k个构件组成的复合铰链,有(k-1)个转动副。
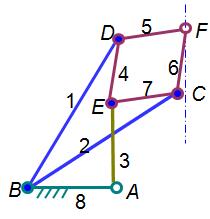
正确计算
B、C、D、E处为复合铰链,转动副数均为2。
n=7,PL=10,PH=0 F=3n-2PL-PH=3*7-2*10=1
准确识别复合铰链举例
关键:分辨清楚哪几个构件在同一处形成了转动副

● 虚约束(Redundant constraint, Passive constraint)
定义:机构中不起独立限制作用的重复约束。
计算具有虚约束的机构的自由度时,应先将机构中引入虚约束的运动副或运动链部分除去。
虚约束发生的场合
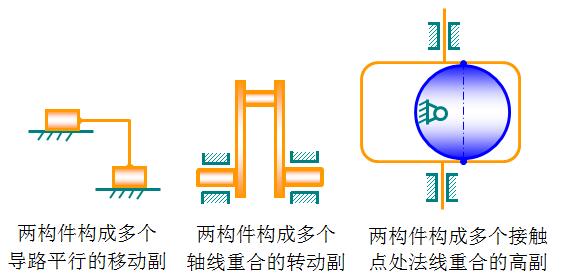
⑴ 两构件间构成多个运动副
⑵ 两构件上某两点间的距离在运动过程中始终保持不变
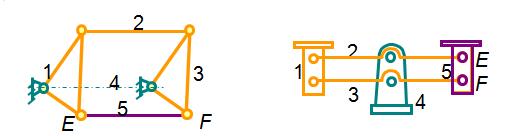
未去掉虚约束时 F=3n-2PL-PH=3*4-2*6=0
附加的构件5和其两端的转动副E、F提供的自由度
F=3*1-2*2=-1
即引入了一个约束,但这个约束对机构的运动不起实际约束作用,为虚约束。去掉虚约束后 F=3n-2PL-PH=3*3-2*4=1
⑶ 联接构件与被联接构件上联接点的轨迹重合
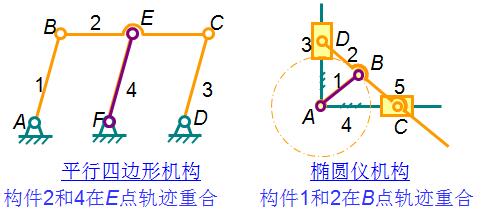
附加的构件4和其两端的转动副E、F以及附加的构件1和其两端的转动副A、B提供的自由度 F=3*1-2*2=-1
即引入了一个约束,但这个约束对机构的运动不起实际约束作用,为虚约束。去掉虚约束后 F= 3n-2PL-PH=3*3-2*4=1
⑷ 机构中对传递运动不起独立作用的对称部分
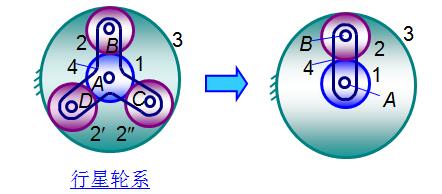
对称布置的两个行星轮2'和2''以及相应的两个转动副D、C和4个平面高副提供的自由度 F=3*2-2*2-1*4=-2
即引入了两个虚约束。
未去掉虚约束时 F= 3n-2PL-PH=3*5-2*5-1*6=-1
去掉虚约束后 F= 3n-2PL-PH=3*3-2*3-1*2=1
虚约束的作用
⑴ 改善构件的受力情况,分担载荷或平衡惯性力,如多个行星轮。
⑵ 增加结构刚度,如轴与轴承、机床导轨。
⑶ 提高运动可靠性和工作的稳定性,如机车车轮联动机构。
注意:机构中的虚约束都是在一定的几何条件下出现的,如果这些几何条件不满足,则虚约束将变成实际有效的约束,从而使机构不能运动。
例:计算包装机送纸机构的自由度
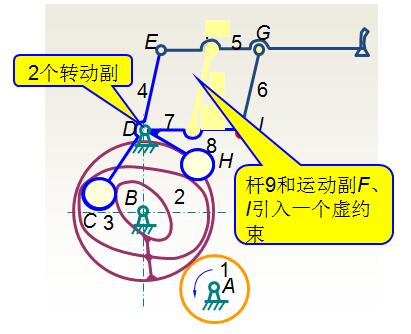

例:计算机构的自由度
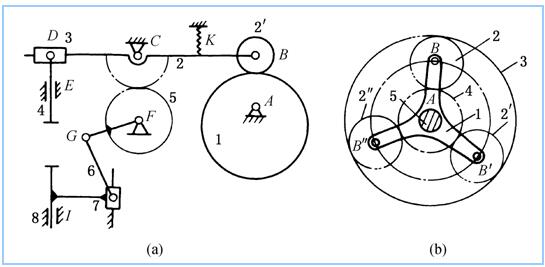
(a) F =3×7-2×9-2=1
(b) F =3×3-2×3-2=1


